数学Ⅰ・A
元河合塾
大竹 真一 先生
長年にわたり河合塾講師として受験生を指導。旺文社の『全国大学入試問題正解』の解答者・巻頭言執筆者であり、受験生向けの参考書・月刊誌、大学の教科書など多数の著書がある。また、大学でも教鞭をとっている。
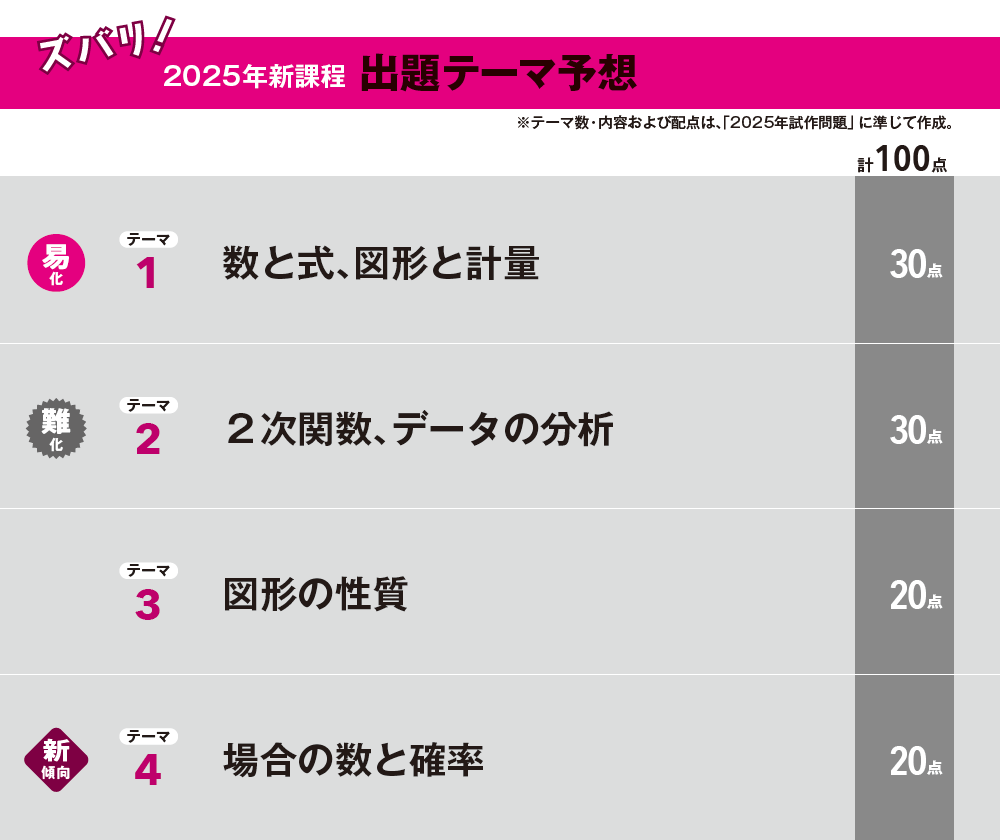
従来の課程にない新しい分野から出題される
新課程による2025年の共通テストは、数学Ⅰ・Aの分野を見る限りは大幅な変更がないだろう。したがって、全体的な構成・内容は従来の共通テストと同様のものになると考えられるが、この新課程では分野によって従来の課程になかった新たな内容が付加される。問題はこの内容も含めた範囲で作成されるので、過去の共通テストでは見られなかった形をとる可能性が大きい。そのため、過去問研究だけでは十分とは言えず、決して多くはないが新たに付加された内容とその学習の着眼点も含め、新たな共通テスト対策を考える必要があるだろう。

● データの分析
傾向
日常の事象を題材として、新課程で新たに加わった外れ値・仮説検定に関するものも出題されるだろう。外れ値を調べて散布図や箱ひげ図に整理し、そこからデータの傾向、事象の特徴を考察する。あるいは、仮説検定の考え方から、仮説の妥当性を判断する問題などが予想される。
対策
ポイントは、「日常生活の事象を数学的に扱うための表現にすること」「数式やグラフなど数学の道具で処理すること」である。まず、教科書などにある基本的な問題について、「事象のどのような数量に着目し、どのような手順で処理するか?」を念頭において解いてみよう。問題の構造は単純なので、数題解くうちに、着目する数量と処理する手順が見えてくるはずである。
● 場合の数と確率
傾向
日常生活で見られる事象の場合の数や確率が考えられる。したがって、問題文は国公立大2次試験のような素朴な文ではなく、長文となるだろう。そのうえで、新課程で新たに加わった期待値について問われる可能性が高い。条件付き確率は、問題の後半で問われることになる。
対策
問題文が長いぶん、読解力が問われることになる。問題文を分析して、与えられている条件・状況、求めるべき確率を知ることが必要である。じっくりと考えつつ読み解くことに慣れてくると、読む時間の短縮にもなる。確率を求める方法を多面的に考察することも、深い理解につながる。期待値の過去問は、共通テストにはないが、センター試験では出題されている。
● 数と式
傾向
単に計算すればよいものでなく、文字係数の方程式・不等式が主題になると思われる。その際、解の条件に、有理数・無理数など「整数」に関係する内容が問われるかもしれない。「整数」は共通テストの出題範囲にないが、素朴な内容か誘導が付くなら出題されるかもしれない。
対策
「整数」は数学Aの「数学と人間の活動」の単元に含まれ、この単元は出題の範囲外であるから、基本的な計算処理で済むはずである。誘導付きならこれも無理のないものだろうから、題意を把握すれば内容は難しくはならないと思われる。2次試験の数学Aでも全範囲を含まないという大学は少ないので、高校の授業などで機会があるたびに「整数」を意識的に学んでほしい。
●図形と計量
傾向
三角比に関する定理・公式、図形への応用、立体に関する計量など、図形の総合問題が出題されよう。三角形の合同・相似などの図形的な定理と、正弦定理・余弦定理などの数式で表される公式が混在するが、これらから得た結果を統合的・発展的に考察することが求められる。
対策
定理・公式は使い方が重要だ。問題演習の際に、「どこで、どの定理・公式を、どう使うか?」と迷うことは多い。この対策としては、「公式そのものについて、どのような働きをするのか?」を事前に知っておくことである。例えば、「正弦定理には、辺と角の関係という側面と、辺・角と外接円の関係という側面がある」と知っておくだけで、活躍する場は広がるはずだ。


共通テスト&センター試験
過去問はこう使う!
演習開始時期:12月中旬~
目標使用量:4回分

共通テストの過去問は2021年から4年分あるが、2022年は平均点が低く、考えにくい問題がかなり多いので、この年は参考程度にして、安定した内容だった残り3年分を中心に使おう。共通テストの持つ特徴を知って慣れることが目標であるが、余裕があればセンター試験も3年分ぐらいはやってみるとよい。過去問は、弱点分野のチェックにも効果的である。

共通テストの過去問集を使うとき、それほど多くはないと思うが、新課程に対応しているかが気になるところだ。その意味で、新課程の範囲を考慮して作成された模試は、本番に最も近い雰囲気を持っていると言える。弱点・苦手分野が判明したら補強をしていくが、その分野は基礎ができていない場合が多いので、教科書で定義や定理・公式などを復習する必要がある。
この続きを読むには

に登録(無料)が必要です
まなびIDに登録すると、
パスナビの記事が読み放題!!
さらに旺文社のサービスで
- Point 1過去問が1年分無料で閲覧できる!
- Point 2自分だけの志望大学リストを作成可能!
- Point 3英検の自己採点が簡単にできる!
この他にも便利な機能が!
詳しくはこちら
受験お役立ち記事を探す
- 受験生必見!勉強・生活・メンタルを最適化する5つのTo do2025/3/17合格への近道はここに!
勉強法・生活環境の見直し・メンタルについてなど、志望校合格に必要な5つのTo doを紹介。今すぐ始められる実践的アドバイス満載!2025/3/17
- 志望校合格と青春の両立!その成功事例と効果的な学習戦略2025/3/17部活と勉強を両立させる方法を知りたい人必見!
厚木高校の生徒がどのように受験と部活を両立しているのか、具体的な成功事例と共に、時間管理のコツや効果的な勉強法を解説します。2025/3/17
- 学習計画が合否を分ける!受験までの学習計画の立て方のポイント2025/3/17受験勉強を成功させるには、計画的な学習が不可欠!螢雪手帳を活用して学習目標と計画を立てましょう。
また、時期ごとの学習計画の立て方、学習法のポイントについても詳しく紹介します。2025/3/17
- 受験生必見!勉強・生活・メンタルを最適化する5つのTo do2025/3/17合格への近道はここに!
勉強法・生活環境の見直し・メンタルについてなど、志望校合格に必要な5つのTo doを紹介。今すぐ始められる実践的アドバイス満載!2025/3/17
- 志望校合格と青春の両立!その成功事例と効果的な学習戦略2025/3/17部活と勉強を両立させる方法を知りたい人必見!
厚木高校の生徒がどのように受験と部活を両立しているのか、具体的な成功事例と共に、時間管理のコツや効果的な勉強法を解説します。2025/3/17
- 学習計画が合否を分ける!受験までの学習計画の立て方のポイント2025/3/17受験勉強を成功させるには、計画的な学習が不可欠!螢雪手帳を活用して学習目標と計画を立てましょう。
また、時期ごとの学習計画の立て方、学習法のポイントについても詳しく紹介します。2025/3/17
- 受験生必見!勉強・生活・メンタルを最適化する5つのTo do2025/3/17合格への近道はここに!
勉強法・生活環境の見直し・メンタルについてなど、志望校合格に必要な5つのTo doを紹介。今すぐ始められる実践的アドバイス満載!2025/3/17
- 志望校合格と青春の両立!その成功事例と効果的な学習戦略2025/3/17部活と勉強を両立させる方法を知りたい人必見!
厚木高校の生徒がどのように受験と部活を両立しているのか、具体的な成功事例と共に、時間管理のコツや効果的な勉強法を解説します。2025/3/17
- 学習計画が合否を分ける!受験までの学習計画の立て方のポイント2025/3/17受験勉強を成功させるには、計画的な学習が不可欠!螢雪手帳を活用して学習目標と計画を立てましょう。
また、時期ごとの学習計画の立て方、学習法のポイントについても詳しく紹介します。2025/3/17
 2024年12月号より転載
2024年12月号より転載





